Idempotent functions
题面翻译
给定一个定义域为 [1,n] 的函数 f(x) ,并告诉你 f(1),f(2)…f(n−1),f(n),定义 f(k)(x)=f(f(k−1)(x)) 。求一个最小的 k 使得 ∀x∈[1,n] ,都有 f(k)(f(k)(x))=f(k)(x) 。
第一行输入一个正整数 n(1≤n≤200) ,第二行 n 个正整数表示 f(i)(1≤f(i)≤n) 。
题目描述
Some time ago Leonid have known about idempotent functions. Idempotent function defined on a set 1,2,...,n is such function 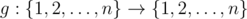 , that for any
, that for any 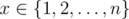 the formula g(g(x))=g(x) holds.
the formula g(g(x))=g(x) holds.
Let's denote as f(k)(x) the function f applied k times to the value x . More formally, f(1)(x)=f(x) , f(k)(x)=f(f(k−1)(x)) for each k>1 .
You are given some function 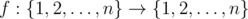 . Your task is to find minimum positive integer k such that function f(k)(x) is idempotent.
. Your task is to find minimum positive integer k such that function f(k)(x) is idempotent.
输入格式
In the first line of the input there is a single integer n ( 1<=n<=200 ) — the size of function f domain.
In the second line follow f(1),f(2),...,f(n) ( 1<=f(i)<=n for each 1<=i<=n ), the values of a function.
输出格式
Output minimum k such that function f(k)(x) is idempotent.
样例 #1
样例输入 #1
4
1 2 2 4
样例输出 #1
1
样例 #2
样例输入 #2
3
2 3 3
样例输出 #2
2
样例 #3
样例输入 #3
3
2 3 1
样例输出 #3
3
提示
In the first sample test function f(x)=f(1)(x) is already idempotent since f(f(1))=f(1)=1 , f(f(2))=f(2)=2 , f(f(3))=f(3)=2 , f(f(4))=f(4)=4 .
In the second sample test:
- function f(x)=f(1)(x) isn't idempotent because f(f(1))=3 but f(1)=2 ;
- function f(x)=f(2)(x) is idempotent since for any x it is true that f(2)(x)=3 , so it is also true that f(2)(f(2)(x))=3 .
In the third sample test:
- function f(x)=f(1)(x) isn't idempotent because f(f(1))=3 but f(1)=2 ;
- function f(f(x))=f(2)(x) isn't idempotent because f(2)(f(2)(1))=2 but f(2)(1)=3 ;
- function f(f(f(x)))=f(3)(x) is idempotent since it is identity function: f(3)(x)=x for any
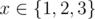 meaning that the formula f(3)(f(3)(x))=f(3)(x) also holds.
meaning that the formula f(3)(f(3)(x))=f(3)(x) also holds.
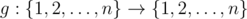 , that for any
, that for any 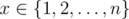 the formula holds.
the formula holds.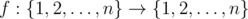 . Your task is to find minimum positive integer such that function is idempotent.
. Your task is to find minimum positive integer such that function is idempotent.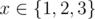 meaning that the formula also holds.
meaning that the formula also holds.
