Infinite Inversions

题面翻译

现在有一个由所有正整数组成的无限递增序列： $p = {1,2,3,...}$ 。

对这个序列执行 $n$ 次交换操作。每次一个操作，给出两个整数 $a,b$ ，交换位置 $a$ 和 $b$ 处的元素。

你的任务是在所有操作结束后，输出最终序列的逆序对个数，即满足 $i < j$ 且 $p_i > p_j$ 的有序数对 $(i,j)$ 的数量。

题目描述

There is an infinite sequence consisting of all positive integers in the increasing order: $p={1,2,3,...}$ . We performed $n$ swap operations with this sequence. A $swap(a,b)$ is an operation of swapping the elements of the sequence on positions $a$ and $b$ . Your task is to find the number of inversions in the resulting sequence, i.e. the number of such index pairs $(i,j)$ , that i&lt;j and p_{i}&gt;p_{j} .

输入格式

The first line contains a single integer $n$ ( $1<=n<=10^{5}$ ) — the number of swap operations applied to the sequence.

Each of the next $n$ lines contains two integers $a_{i}$ and $b_{i}$ ( $1<=a_{i},b_{i}<=10^{9}$ , $a_{i}≠b_{i}$ ) — the arguments of the swap operation.

输出格式

Print a single integer — the number of inversions in the resulting sequence.

样例 #1

样例输入 #1

2
4 2
1 4

样例输出 #1

4

样例 #2

样例输入 #2

3
1 6
3 4
2 5

样例输出 #2

15

提示

In the first sample the sequence is being modified as follows: 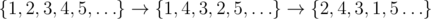. It has 4 inversions formed by index pairs $(1,4)$ , $(2,3)$ , $(2,4)$ and $(3,4)$ .