A Heap of Heaps

题面翻译

有一个小根堆，但是因为奇奇怪怪的原因，这个堆变成了一个k叉堆，而且不一定是合法的（即有若干个节点小于它的父亲）。问现在这个堆有多少不合法的元素。

题目描述

Andrew skipped lessons on the subject 'Algorithms and Data Structures' for the entire term. When he came to the final test, the teacher decided to give him a difficult task as a punishment.

The teacher gave Andrew an array of $n$ numbers $a_{1}$ , $...$ , $a_{n}$ . After that he asked Andrew for each $k$ from 1 to $n-1$ to build a $k$ -ary heap on the array and count the number of elements for which the property of the minimum-rooted heap is violated, i.e. the value of an element is less than the value of its parent.

Andrew looked up on the Wikipedia that a $k$ -ary heap is a rooted tree with vertices in elements of the array. If the elements of the array are indexed from 1 to $n$ , then the children of element $v$ are elements with indices $k(v-1)+2$ , $...$ , $kv+1$ (if some of these elements lie outside the borders of the array, the corresponding children are absent). In any $k$ -ary heap every element except for the first one has exactly one parent; for the element 1 the parent is absent (this element is the root of the heap). Denote $p(v)$ as the number of the parent of the element with the number $v$ . Let's say that for a non-root element $v$ the property of the heap is violated if a_{v}<a_{p(v)} .

Help Andrew cope with the task!

输入格式

The first line contains a single integer $n$ ( $2<=n<=2·10^{5}$ ).

The second line contains $n$ space-separated integers $a_{1}$ , $...$ , $a_{n}$ ( $-10^{9}<=a_{i}<=10^{9}$ ).

输出格式

in a single line print $n-1$ integers, separate the consecutive numbers with a single space — the number of elements for which the property of the $k$ -ary heap is violated, for $k=1$ , $2$ , $...$ , $n-1$ .

样例 #1

样例输入 #1

5
1 5 4 3 2

样例输出 #1

3 2 1 0

样例 #2

样例输入 #2

6
2 2 2 2 2 2

样例输出 #2

0 0 0 0 0

提示

Pictures with the heaps for the first sample are given below; elements for which the property of the heap is violated are marked with red.

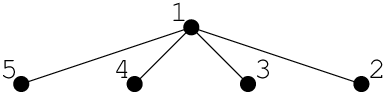In the second sample all elements are equal, so the property holds for all pairs.