Tavas on the Path

题面翻译

给定一棵 $n$ 个节点的树，每条边有边权。

有 $m$ 个询问，形式为 $(u,v,l)$，求 $u$ 到 $v$ 的路径，假设长度为 $p$，第 $i$ 条边权值为 $x_i$，构造一个长度为 $p$ 的 01串 $s$，如果 $x_i\ge l$，那么 $s_i=1$，否则 $s_i=0$。

对于得到的串 $s$，假设它有 $k$ 段连续的 1，第 $i$ 段长度为 $p_i$，那么要你输出所有 $f_{p_i}$ 的和，其中 $f$ 数组一开始就给出。

题目描述

Tavas lives in Tavaspolis. Tavaspolis has $n$ cities numbered from $1$ to $n$ connected by $n-1$ bidirectional roads. There exists a path between any two cities. Also each road has a length.

Tavas' favorite strings are binary strings (they contain only 0 and 1). For any binary string like $s=s_{1}s_{2}...\ s_{k}$ , $T(s)$ is its $Goodness$ . $T(s)$ can be calculated as follows:

Consider there are exactly $m$ blocks of $1$ s in this string (a block of $1$ s in $s$ is a maximal consecutive substring of $s$ that only contains $1$ ) with lengths $x_{1},x_{2},...,x_{m}$ .

Define 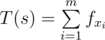where $f$ is a given sequence (if $m=0$ , then $T(s)=0$ ).

Tavas loves queries. He asks you to answer $q$ queries. In each query he gives you numbers $v,u,l$ and you should print following number:

Consider the roads on the path from city $v$ to city $u$ : $e_{1},e_{2},...,e_{x}$ .

Build the binary string $b$ of length $x$ such that: $b_{i}=1$ if and only if $l<=w(e_{i})$ where $w(e)$ is the length of road $e$ .

You should print $T(b)$ for this query.

输入格式

The first line of input contains integers $n$ and $q$ ( $2<=n<=10^{5}$ and $1<=q<=10^{5}$ ).

The next line contains $n-1$ space separated integers $f_{1},f_{2},...,f_{n-1}$ ( $|f_{i}|<=1000$ ).

The next $n-1$ lines contain the details of the roads. Each line contains integers $v,u$ and $w$ and it means that there's a road between cities $v$ and $u$ of length $w$ ( $1<=v,u<=n$ and $1<=w<=10^{9}$ ).

The next $q$ lines contain the details of the queries. Each line contains integers $v,u,l$ ( $1<=v,u<=n$ , $v≠u$ and $1<=l<=10^{9}$ ).

输出格式

Print the answer of each query in a single line.

样例 #1

样例输入 #1

2 3
10
1 2 3
1 2 2
1 2 3
1 2 4

样例输出 #1

10
10
0

样例 #2

样例输入 #2

6 6
-5 0 0 2 10
1 2 1
2 3 2
3 4 5
4 5 1
5 6 5
1 6 1
1 6 2
1 6 5
3 6 5
4 6 4
1 4 2

样例输出 #2

10
-5
-10
-10
-5
0