#P4755. Landmarks
Landmarks
Landmarks
题面翻译
题意简述
有 根柱子支撑着一栋老房子。这些柱子位于坐标为 的点上。对于位于 的柱子,我们知道它的承重系数 。位于 两个位置的柱子的承重系数可以认为是 。
对于位于 的柱子,需要承重的部分为它到两边柱子距离的一半,即 。当该长度超过 时该柱子会坍塌。因此,会不断地有柱子坍塌。而位于 和 的柱子不会坍塌。
当只剩下位于 和 的柱子时,这栋老房子将会坍塌。
现在要求你往建筑中间加一根柱子,使得房子不会坍塌。可以在原有柱子的位置替换掉原有的柱子。求房子不坍塌的情况下,这根新加的柱子的承重系数的最小值。
输入格式
第一行包含一个正整数 ,表示会坍塌的柱子数量。
第二行包含 个整数 表示柱子的位置。
第三行包含 个整数 表示柱子的承重系数。
保证 , , ,
输出格式
输出一个误差在 以内的浮点数,表示使得房子不坍塌的情况下,添加柱子的承重系数最小值。
如果房子原本就不会坍塌,则输出 。
题目描述
We have an old building with columns in a row. These columns support the ceiling. These columns are located in points with coordinates 0=x_{0}<x_{1}<...<x_{n}<x_{n+1} . The leftmost and the rightmost columns are special, we will call them bearing, the other columns are ordinary.
For each column we know its durability . Let's consider an ordinary column with coordinate . Let's assume that the coordinate of the closest to it column to the left (bearing or ordinary) is and the coordinate of the closest to it column to the right (also, bearing or ordinary) is . In this task let's assume that this column supports the segment of the ceiling from point 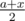 to point
to point 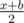 (here both fractions are considered as real division). If the length of the segment of the ceiling supported by the column exceeds , then the column cannot support it and it crashes after a while, and after that the load is being redistributeed between the neighbouring columns according to the same principle.
(here both fractions are considered as real division). If the length of the segment of the ceiling supported by the column exceeds , then the column cannot support it and it crashes after a while, and after that the load is being redistributeed between the neighbouring columns according to the same principle.
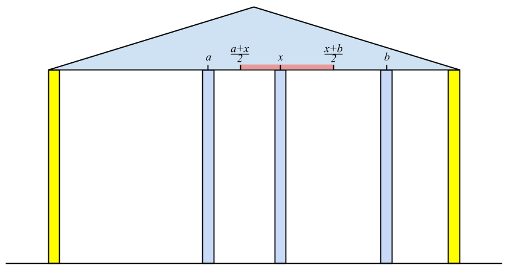 Thus, ordinary columns will be crashing for some time until the process stops at some state. One can prove that the set of the remaining columns doesn't depend on the order in which columns crash. If there are only two bearing columns left in the end, then we assume that the whole construction crashes under the weight of the roof. But if at least one ordinary column stays in addition to the bearing ones, then the building doesn't crash.
Thus, ordinary columns will be crashing for some time until the process stops at some state. One can prove that the set of the remaining columns doesn't depend on the order in which columns crash. If there are only two bearing columns left in the end, then we assume that the whole construction crashes under the weight of the roof. But if at least one ordinary column stays in addition to the bearing ones, then the building doesn't crash.
To make the building stronger, we can add one extra ordinary column of arbitrary durability at any (not necessarily integer) point 0<x'<x_{n+1} . If point is already occupied by an ordinary column, it is replaced by a new one.
Your task is to find out: what minimal durability can the added column have so that the building doesn't crash?
输入格式
The first line contains integer ( ) — the number of ordinary columns.
The second line contains integers ( , x_{i}<x_{i+1} for , ) — the coordinates of the columns.
The third line contains integers ( ).
输出格式
Print a single number — the minimum possible durability of the column that you need to add in order to make the building stay. If you do not have to add the column, please print . Your answer will be checked with the relative or absolute error .
样例 #1
样例输入 #1
2
0 20 40 100
15 40
样例输出 #1
10
样例 #2
样例输入 #2
3
0 4 10 28 30
9 13 5
样例输出 #2
0