#P4823. DNA Alignment
DNA Alignment
DNA Alignment
题面翻译
给定一个n长度的由、、、四种序列构成的序列。问有多少种方案,构造另一种序列,使得两种序列在过程中,两者相同的位数总和最大。操作即移位操作,两者分别移动,然后求相同位的个数。
题目描述
Vasya became interested in bioinformatics. He's going to write an article about similar cyclic DNA sequences, so he invented a new method for determining the similarity of cyclic sequences.
Let's assume that strings and have the same length , then the function is defined as the number of positions in which the respective symbols of and are the same. Function can be used to define the function of Vasya distance :
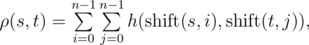 where
where  is obtained from string , by applying left circular shift times. For example, ρ("AGC","CGT")= $ h("AGC","CGT")+h("AGC","GTC")+h("AGC","TCG")+ $ $ h("GCA","CGT")+h("GCA","GTC")+h("GCA","TCG")+ $ $ h("CAG","CGT")+h("CAG","GTC")+h("CAG","TCG")= $ Vasya found a string of length on the Internet. Now he wants to count how many strings there are such that the Vasya distance from the string attains maximum possible value. Formally speaking, must satisfy the equation:
is obtained from string , by applying left circular shift times. For example, ρ("AGC","CGT")= $ h("AGC","CGT")+h("AGC","GTC")+h("AGC","TCG")+ $ $ h("GCA","CGT")+h("GCA","GTC")+h("GCA","TCG")+ $ $ h("CAG","CGT")+h("CAG","GTC")+h("CAG","TCG")= $ Vasya found a string of length on the Internet. Now he wants to count how many strings there are such that the Vasya distance from the string attains maximum possible value. Formally speaking, must satisfy the equation:  .
.
Vasya could not try all possible strings to find an answer, so he needs your help. As the answer may be very large, count the number of such strings modulo .
输入格式
The first line of the input contains a single integer ( ).
The second line of the input contains a single string of length , consisting of characters "ACGT".
输出格式
Print a single number — the answer modulo .
样例 #1
样例输入 #1
1
C
样例输出 #1
1
样例 #2
样例输入 #2
2
AG
样例输出 #2
4
样例 #3
样例输入 #3
3
TTT
样例输出 #3
1
提示
Please note that if for two distinct strings and values и are maximum among all possible , then both strings must be taken into account in the answer even if one of them can be obtained by a circular shift of another one.
In the first sample, there is ρ("C","C")=1 , for the remaining strings of length 1 the value of is 0.
In the second sample, $ ρ("AG","AG")=ρ("AG","GA")=ρ("AG","AA")=ρ("AG","GG")=4 $ .
In the third sample, ρ("TTT","TTT")=27

