Drazil and Factorial

题面翻译

题目描述 Drazil正在和Varda一起玩数学游戏。

让我们定义正整数x作为其数字的阶乘的乘积。例如，F(135)=1!*3!*5!=720。

首先，他们选择一个十进制数a，a是一个由n个数字组成的数。此数字可能以前导零开头。然后他们要找到最大正数x，x满足以下两个条件：

1.x不包含任何数字0和数字1。

2.F(x)=F(a)。

帮朋友找到这样的号码。

输入输出格式 输入格式： 第一行包含一个整数n（1<=n<=15）。

第二行包含一个长度n的数字a。a至少有一位数字。数字a可能包含前导零。

输出格式： 输出满足上述条件的最大可能整数。在这个数字十进制表示中应该没有零和1。

题目描述

Drazil is playing a math game with Varda.

Let's define 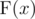for positive integer $x$ as a product of factorials of its digits. For example, .

First, they choose a decimal number $a$ consisting of $n$ digits that contains at least one digit larger than $1$ . This number may possibly start with leading zeroes. Then they should find maximum positive number $x$ satisfying following two conditions:

1. $x$ doesn't contain neither digit $0$ nor digit $1$ .

2. = .

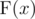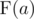Help friends find such number.

输入格式

The first line contains an integer $n$ ( $1<=n<=15$ ) — the number of digits in $a$ .

The second line contains $n$ digits of $a$ . There is at least one digit in $a$ that is larger than $1$ . Number $a$ may possibly contain leading zeroes.

输出格式

Output a maximum possible integer satisfying the conditions above. There should be no zeroes and ones in this number decimal representation.

样例 #1

样例输入 #1

4
1234

样例输出 #1

33222

样例 #2

样例输入 #2

3
555

样例输出 #2

555

提示

In the first case,