Strongly Connected City 2

题面翻译

给一个无向图，你需要给所有边定向，使定向之后存在最多的点对 $(a,b)$ 使得从 $a$ 能到 $b$

题目描述

Imagine a city with $n$ junctions and $m$ streets. Junctions are numbered from $1$ to $n$ .

In order to increase the traffic flow, mayor of the city has decided to make each street one-way. This means in the street between junctions $u$ and $v$ , the traffic moves only from $u$ to $v$ or only from $v$ to $u$ .

The problem is to direct the traffic flow of streets in a way that maximizes the number of pairs $(u,v)$ where $1<=u,v<=n$ and it is possible to reach junction $v$ from $u$ by passing the streets in their specified direction. Your task is to find out maximal possible number of such pairs.

输入格式

The first line of input contains integers 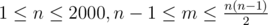$n$ and $m$ , (), denoting the number of junctions and streets of the city.

Each of the following $m$ lines contains two integers $u$ and $v$ , ( $u≠v$ ), denoting endpoints of a street in the city.

Between every two junctions there will be at most one street. It is guaranteed that before mayor decision (when all streets were two-way) it was possible to reach each junction from any other junction.

输出格式

Print the maximal number of pairs $(u,v)$ such that that it is possible to reach junction $v$ from $u$ after directing the streets.

样例 #1

样例输入 #1

5 4
1 2
1 3
1 4
1 5

样例输出 #1

13

样例 #2

样例输入 #2

4 5
1 2
2 3
3 4
4 1
1 3

样例输出 #2

16

样例 #3

样例输入 #3

2 1
1 2

样例输出 #3

3

样例 #4

样例输入 #4

6 7
1 2
2 3
1 3
1 4
4 5
5 6
6 4

样例输出 #4

27

提示

In the first sample, if the mayor makes first and second streets one-way towards the junction $1$ and third and fourth streets in opposite direction, there would be 13 pairs of reachable junctions: $ {(1,1),(2,2),(3,3),(4,4),(5,5),(2,1),(3,1),(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)} $