CGCDSSQ
题面翻译
给出一个长度为 n(1≤n≤105) 的序列和 q(1≤q≤3×105) 个询问,每个询问输出一行,询问 gcd(al,al+1,...,ar)=x 的 (i,j) 的对数.
ai≤109
感谢@凌幽 提供的翻译
题目描述
Given a sequence of integers a1,...,an and q queries x1,...,xq on it. For each query xi you have to count the number of pairs (l,r) such that 1<=l<=r<=n and gcd(al,al+1,...,ar)=xi .
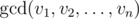 is a greatest common divisor of v1,v2,...,vn , that is equal to a largest positive integer that divides all vi .
is a greatest common divisor of v1,v2,...,vn , that is equal to a largest positive integer that divides all vi .
输入格式
Given a sequence of integers a1,...,an and q queries x1,...,xq on it. For each query xi you have to count the number of pairs (l,r) such that 1<=l<=r<=n and gcd(al,al+1,...,ar)=xi .
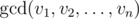 is a greatest common divisor of v1,v2,...,vn , that is equal to a largest positive integer that divides all vi .
is a greatest common divisor of v1,v2,...,vn , that is equal to a largest positive integer that divides all vi .
输出格式
For each query print the result in a separate line.
样例 #1
样例输入 #1
3
2 6 3
5
1
2
3
4
6
样例输出 #1
1
2
2
0
1
样例 #2
样例输入 #2
7
10 20 3 15 1000 60 16
10
1
2
3
4
5
6
10
20
60
1000
样例输出 #2
14
0
2
2
2
0
2
2
1
1
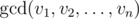 is a greatest common divisor of , that is equal to a largest positive integer that divides all .
is a greatest common divisor of , that is equal to a largest positive integer that divides all .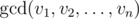 is a greatest common divisor of , that is equal to a largest positive integer that divides all .
is a greatest common divisor of , that is equal to a largest positive integer that divides all .
